
Examinee Collusion: Primary vs Secondary
It’s October 30, 2017, and collusion is all over the news today… but I want to talk about a different kind of collusion. That is, non-independent test taking. In the field of psychometric forensics, examinee collusion refers to cases where an examinee takes a test with some sort of external help in obtaining the correct answers. There are several possibilities:
- Low ability examinees copy off a high ability examinee (known as the Source); could be unbeknownst to the source.
- Examinees work together and pool their answers.
- Examinees receive answers from a present third party, such as a friend outside with Bluetooth, a teacher, or a proctor.
- Multiple examinees obtaining answers from a brain dump site, known as preknowledge; while not strictly collusion, we’d likely find similar answer patterns in that group, even if they never met each other.
The research on the field has treated all of these more or less equivalently, and as a group. I’d like to argue that we stop doing that. Why? The data patterns can be different, and can therefore be detected (or not detected) by different types of forensics. Most importantly, some collusion indices are designed specifically for some cases, and we need to treat them as such. More broadly, perhaps we need a theoretical background on types of collusion – part of an even broader theory on types of invalid test-taking – as a basis to fit, evaluate, and develop indices.
What do I mean by this? Well, some collusion indices are explicitly designed around the assumption that there is a Source and a copier(s). The strongest examples are the K-variants (Sotaridona, 2003) and Wollack’s (1997) omega. Other indices do not assume this, such as Bellezza & Bellezza (1989); they simply look for similarities in responses, either on errors alone or on both errors and correct answers.
Collusion indices, if you’re not familiar with them, evaluate each possible pair of examinees and look for similar response patterns; if you have 1000 examinees, there are (1000 x 9999)/2 = 4,999,500 pairs. If you use an index that evaluates the two directions separately (Examinee 1 is Source and 2 is Copier, then 2 is Source and 1 is Copier), you are calculating the index 9,999,000 times on this relatively small data set.
Primary vs. Secondary Collusion
Consider the first case above, which is generally of interest. I’d like to delineate the difference between primary collusion and secondary collusion. Primary collusion is what we are truly trying to find: if examinees are copying off another examinee. Some indices are great at finding this. But there is also secondary collusion; if multiple examinees are copiers, they will also have very similar response patterns, though the data signature will be different than if paired with the Source. Indices designed to find primary collusion might not be as strong as finding this; rightly so, you might argue.
The other three cases above, I’d argue, are also secondary collusion. There is no true Source present in the examinees, but we are certainly going to find unusually similar response patterns. Indices that are explicitly designed to find the Source are not going to have the statistical power that was intended. They require a slightly different set of assumptions, different interpretations, and different calculations.
What might the different calculations be? That’s for another time. I’m currently working through a few ideas. The most recent is based on the discovery that the highly regarded S2 index (Sotaridona, 2003) makes assumptions that are regularly violated in real data, and that the calculations need to be modified. I’ll be integrating the new index into SIFT.
An example of examinee collusion
To demonstrate, I conducted a brief simulation study, part of a much larger study to be published at a future date. I took a data set of a national educational assessment (N=16,666, 50 MC items), randomly selected 1,000 examinees, randomly assigned them to one of 10 locations, and then created a copying situation in one location. To do this, I found the highest ability examinee at that location and the lowest 50, then made those low 50 copy the answers off the high examinee for the 25 hardest items. This is a fairly extreme and clear-cut example, so we’d hope that the collusion indices pick up on such an obvious data signature.
Let’s start by investigating that statement. This is an evaluation of power, which is the strength of a statistical test to find something when something is actually there (though technically, not all of these indices are statistical tests). We hope that we can find all 50 instances of primary collusion as well as most of the secondary collusion. As of today, SIFT calculates 15 collusion indices; for a full description of these, download a free copy and check out the manual.
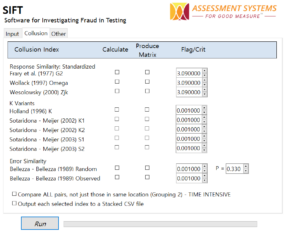
What does this all mean?
Well, my original point was that we need to differentiate the Primary and Secondary cases of collusion, and evaluate them separately when we can. An even broader point was that we need a specific framework on types of invalid test instances and the data signatures they each leave, but that’s worth an article on its own.
If the topic of index comparison is interesting to you, check out the chapter by Zopluogu (2016). He also found the power for S2 to be low, and the Type I errors to be conservative, though the Type II were not reported there. That research stemmed from a dissertation at the University of Minnesota, which probably has a fuller treatment; my goal here is not to fully repeat that extensive study, but to provide some interesting interpretations.
Nathan Thompson, PhD
Latest posts by Nathan Thompson, PhD (see all)
- What is a T score? - April 15, 2024
- Item Review Workflow for Exam Development - April 8, 2024
- Likert Scale Items - February 9, 2024
